 |
 |
 |
|
||||||||||||||||||||||||
 | ||||||||||||||||||||||||
 | ||||||||||||||||||||||||
 | ||||||||||||||||||||||||
Interactive Java Tutorials
Colocalization of Fluorophores in Confocal Microscopy
Two or more fluorescence emission signals can often overlap in digital images recorded by confocal microscopy due to their close proximity within the specimen. This effect is known as colocalization and usually occurs when fluorescently labeled molecules bind to targets that lie in very close or identical spatial positions. This interactive tutorial explores the quantitative analysis of colocalization in a wide spectrum of specimens that were specifically designed either to demonstrate the phenomenon, or to alternatively provide examples of fluorophore targets that lack any significant degree of colocalization.
The tutorial initializes with a randomly chosen confocal microscopy dual or triple labeled fluorescence image appearing in the Specimen Image window and the accompanying red-green (or red-blue) scatterplot graphed two-dimensionally in the adjacent Colocalization Scatterplot coordinate system. Plots of the available channel permutations (Red-Green, Red-Blue, and Green-Blue) can be displayed using the Colocalization Channels set of radio buttons. In addition, each channel in the Specimen Image window can be toggled on or off using the check boxes in the Channels menu. A three-dimensional rendering of the colocalization scatterplot (number of pixels plotted on the z axis) can be obtained by activating the 3D radio button. This view can be rotated within the window using the mouse cursor. Colocalization coefficients automatically displayed beneath the scatterplot graph include Pearson's, Overlap, and Global (k1 and k2), as described below.
In order to operate the tutorial, use the mouse cursor to draw a region of interest in the Colocalization Scatterplot graph. The default area selection tool generates rectangular regions, but elliptical and freehand areas can be chosen with the appropriate Region of Interest radio buttons. Once a region has been selected, an overlay of the colocalized pixels is displayed in the Specimen Image window and the Global colocalization coefficient display changes into the Local (M1 and M2) value calculated within the region of interest. The image Colocalization Overlay view can be toggled between Full Color and Binary views using check boxes. At any point, a new specimen can be selected using the Choose A Specimen pull-down menu. Details of the specimen fluorophore staining protocol and the potential for colocalization are described in the yellow text box at the bottom of the tutorial window.
A quantitative assessment of fluorophore co-localization in confocal optical sections can be obtained using the information obtained from scatterplots and selected regions of interest. Several values are generated using information from the entire scatterplot, while others are derived from pixel values contained within a selected region of interest. Among the variables used to analyze the entire scatterplot is Pearson's correlation coefficient (R(r)), which is one of the standard techniques applied in pattern recognition for matching one image to another in order to describe the degree of overlap between the two patterns. Pearson's correlation coefficient is calculated according to the equation:
 |
(1) |
where S1 is the signal intensity of pixels in the first channel and S2 is the signal intensity of pixels in the second channel. The values S1(average) and S2(average) are the average values of pixels in the first and second channel, respectively. In Pearson's correlation, the average pixel intensity values are subtracted from the original intensity values. As a result, the value of this coefficient ranges from -1 to 1, with a value of -1 representing a total lack of overlap between pixels from the images, and a value of 1 indicating perfect image registration. Pearson's correlation coefficient accounts only for the similarity of shapes between the two images, and does not depend upon image pixel intensity values. When applying this coefficient to co-localization analysis, however, the potentially negative values are difficult to interpret, requiring another approach to clarify analysis results.
A simpler technique often employed to calculate an alternative correlation coefficient involves eliminating the subtraction of average pixel intensity values from the original intensities. Defined formally as the Overlap coefficient (R), this value ranges between 0 and 1 and is not sensitive to intensity variations in the image analysis. The Overlap coefficient is defined as:
 |
(2) |
The product of channel intensities in the numerator returns a significant value only when both values belong to a pixel involved in co-localization (if both intensities are greater than zero). As a result, the numerator in equation (2) is proportional to the number of co-localizing pixels. In a similar manner, the denominator of the Overlap equation is proportional to the number of pixels from both components in the image, regardless of whether co-localization is present (Note: the components are defined as the red and green images or the pixel arrays from channel 1 and channel 2, respectively). A major advantage of the Overlap coefficient is its relative insensitivity to differences in signal intensities between various components of an image, which are often produced by fluorochrome concentration fluctuations, photobleaching, quantum efficiency variations, and non-equivalent electronic channel settings.
The most important disadvantage of using the Overlap coefficient is the strong influence of the ratio between the number of image features in each channel. To alleviate this dependency, the Overlap coefficient is divided into two different sub-coefficients, termed k(1) and k(2) in order to express the degree of co-localization as two separate parameters:
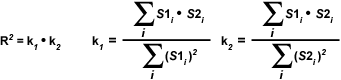 |
(3) |
The overlap coefficients, k(1) and k(2), describe the differences in intensities between the channels, with k(1) being sensitive to the differences in the intensity of channel 2 (green signal), while k(2) depends linearly on the intensity of the pixels from channel 1 (red signal). The equations described thus far are able to generate information about the degree of overlap and can account for intensity variations between the color channels. In order to estimate the contribution of one color channel in the co-localized areas of the image to the overall amount of co-localized fluorescence, an additional set of co-localization coefficients, m(1) and m(2), are defined:
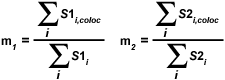 |
(4) |
The co-localization coefficient m(1) is employed to describe the contribution from channel 1 to the co-localized area, while the coefficient m(2) is used to describe the same contribution from channel 2. Note that the variable S1(i,coloc) is equal to S1(i) if S2(i) is greater than zero and vice versa for the variable S2(i,coloc). These coefficients are proportional to the amount of fluorescence of the co-localizing fluorophores in each channel of the composite image, relative to the total fluorescence in that channel. Co-localization coefficients m(1) and m(2) can be determined even when the signal intensities in the two image channels have significantly different levels.
A second pair of co-localization coefficients can be calculated for pixel intensity ranges defined by an area of interest delineated on the scatterplot. The coefficient M(1) is utilized to describe the contribution of the channel 1 fluorophore to the co-localized area, while M(2) is used to describe the contribution of the channel 2 fluorophore. These co-localization coefficients are defined as:
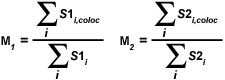 |
(5) |
where S1(i,coloc) equals S1(i) if S2(i) lies within the region of interest thresholds (left and right sides of a rectangular ROI) and equals zero if S2(i) represents a pixel outside the threshold levels. Similarly, S2(i,coloc) equals S2(i) if S1(i) lies within the region of interest thresholds (top and bottom sides of a rectangular ROI) and equals zero if S1(i) is outside the region of interest. In other words, for each channel, the numerator represents the sum of all pixel intensities in that channel that also have a component from the other channel, whereas the denominator represents the sum of all intensities from the channel. These coefficients are proportional to the amount of fluorescence of co-localizing objects in each channel of the composite image, relative to the total fluorescence in that channel.
A majority of the co-localization software analysis programs available commercially are able to calculate the parameters described above, including Pearson's correlation coefficient, the total overlap coefficient, as well as the individual k(x), m(x), and M(x) co-localization coefficients. In addition, many programs contain algorithms to apply background subtraction corrections, generate scatterplots of the entire image, and/or perform the calculations using selected regions of interest on single dual channel composite images or optical stacks along the axial plane. The most important data output from these software packages is the co-localization coefficient, which indicates the relative degree of overlap between signals. For example, a co-localization coefficient value of 0.75 for the fluorophore in channel 1 indicates that the ratio for all channel 1 intensities that have a channel 2 component, divided by the sum of all channel 1 intensities, is 75 percent. This is a relatively high degree of co-localization. Likewise, a value of 0.25 for the channel 2 fluorophore indicates a significantly diminished level of co-localization (equal to one-third of the channel 1 fluorophore).
Contributing Authors
Will Casavan and Yuri Gaidoukevitch - Media Cybernetics, 8484 Georgia Avenue, Suite 200, Silver Spring, Maryland, 20910.
Matthew J. Parry-Hill, Nathan S. Claxton, and Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.
