|
 |
 |
|
||||||||||||||||||||||||
 | ||||||||||||||||||||||||
 | ||||||||||||||||||||||||
 | ||||||||||||||||||||||||
Theory of Confocal Microscopy
Signal-to-Noise Considerations
Optical theory provides that resolution in the microscope is governed by the numerical aperture of the optical system and the wavelength of light used to form the image. In order to be meaningful in practice, however, resolution must be defined in terms of contrast, and it is the number of photons collected from a specimen that ultimately determines the level of signal with respect to measurement uncertainties, and therefore the achievable image contrast. In laser scanning fluorescence confocal microscopy, of biological materials in particular, the signal levels are typically low due to the limited amount of light obtainable from the small fluorophore probe volume in the focused beam.
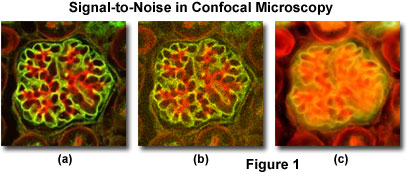
A comparison of typical confocal and widefield microscopy digital images with varying degrees of signal level are presented in Figure 1. Thin optical sections collected with a small pinhole aperture diameter in confocal microscopy produce images having high contrast and relatively low signal-to-noise ratios when substantial fluorescence label is present (Figure 1(a); the specimen is a triple-labeled thin section of mouse kidney). However, at lower probe concentrations, light intensity declines rapidly and the resulting confocal images appear more grainy due to the lowered signal level (Figure 1(b)). A widefield fluorescence image of the specimen illustrated in Figures 1(a) and 1(b) is included (Figure 1(c)) to demonstrate the problem of degrading fluorescence arising from areas away from the objective focal plane.
In any quantitative assessment of imaging capabilities utilizing digital microscopy techniques, including confocal methods, the effect of signal sampling on contrast and resolution must be considered. The measured signal level values do not directly represent the number of photons emitted or scattered by the specimen, but are proportional to that number. Furthermore, each individual sample of signal intensity is only an approximation of the number of collected photons, and will vary with repeated measurement. The variation, referred to as noise, imparts an uncertainty in the quantification of intensity, and therefore in the contrast and resolution of the image data. Although the effects of sampling can be estimated fairly easily, the determination of noise in a single pixel is much more problematic.
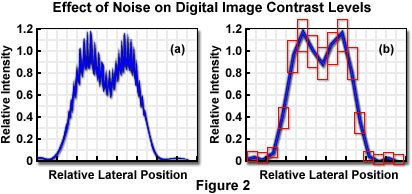
In transmission or reflection contrast mechanisms, the specimen signal intensity (number of photons) is typically very high, and the dominant noise sources are electronic noise in the instrumentation, or in some cases, fluctuations in the illumination intensity. When fluorescence emission is employed for imaging, the photon number is generally extremely small, and statistical variation in the number of detected photons, or Poisson noise, will be the most significant variable. Figure 2 illustrates the effect of noise in adding uncertainty to the sampled intensity values in the Airy pattern resulting from imaging two point-like specimen features.
Rather than beginning with a mathematical assessment of noise and its effects on image characteristics, it is useful to consider conceptually the mechanisms by which noise and the signal-to-noise ratio influence imaging. The uncertainty in intensity determinations, and in measured contrast based on the intensity values, results in an overall reduction in contrast. As any contrast reduction decreases the cut-off distance, degradation in resolution (defined with reference to a given contrast) results from noise in the detected signal. A further mechanism by which the level of noise relative to the signal influences imaging capabilities is in the number of gray levels that can be distinguished in an individual image pixel, which in effect establishes a limit on the dynamic range of the image. The effective dynamic range can be considered to be the ratio of the signal divided by noise. Since noise, because of its Poisson characteristics in the fluorescence microscope, is equivalent to the square root of the mean signal, the dynamic range is the signal divided by the square root of the signal, and is therefore equivalent to the square root of the signal.
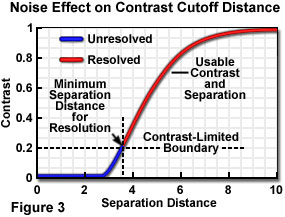
When the contribution of noise to the specimen signal is considered, it essentially raises the signal level "floor", below which insufficient contrast exists between specimen point-like features to enable them to be distinguished as separate. In plotting contrast-distance functions to demonstrate resolution limits, it is common to neglect noise and to assume an infinitely high signal-to-noise ratio and dynamic range. The separation distance required to provide sufficient contrast to "resolve" two image features is increased when noise is considered, and the contrast level required for visibility must be determined with respect to a higher minimum usable contrast level. When the usable contrast range no longer extends to zero, a situation such as that illustrated in Figure 3 exists, in which a constant arbitrary noise level limits the useable contrast and point separation range.
Steps taken to improve resolution by decreasing the size of the focal spot at the specimen will result in a decrease in the number of excitable fluorophores and therefore in the number of photons that can be collected, implying a higher noise level. The increase in noise relative to signal and the reduction in dynamic range limit the resolution improvement that can be achieved by reducing the dimensions of the intensity point spread function (PSF) in the confocal microscope. When the observation volume is decreased by making the point spread function smaller, the sampling period has to be increased to maintain the same signal-to-noise ratio, a strategy that is often not an option due to the deleterious effects of both the increased photon flux on specimen integrity and to fluorophore saturation.
The confocal imaging effect is only strictly obtained with a detector pinhole that is infinitesimally small, producing an image signal level too low to be useful. At the opposite extreme, a very large pinhole chosen to maximize the specimen signal will eliminate the confocal advantage entirely. In practice, an optimum pinhole size must be chosen to maximize the recording of specimen information, taking into consideration the microscope configuration, its mode of operation, and the specimen characteristics.
As stated previously, the overall signal level in biological fluorescence microscopy applications is typically low for several reasons, one of which is that fluorophore photobleaching upon illumination is always a factor, and must be minimized by limiting the total exposure to excitation light. This effectively limits the number of photons available for detection, increasing the significance of signal variation caused by the statistical nature of the detection process. This noise is commonly referred to as shot noise or photon noise and is a result of the particle nature of light and the discrete electrical characteristics of the emitted photons. In effect, the stochastic fluctuation in photon arrival times at the detector is responsible for shot noise. At low signal levels, shot noise reduces the number of gray levels that can be discriminated in an image and has an overall degrading effect on image quality.
When all noise sources are considered, the signal-to-noise ratio (S/N) can be utilized as a measure of overall image quality. If shot noise were the only significant noise component in the detected signal in the confocal microscope, the signal-to-noise ratio would increase directly with increasing pinhole size, enabling the value to be enhanced up to the point at which the pinhole diameter becomes too large to achieve the desired confocal optical sectioning effect. This is not the case, however, and an additional source of statistical noise is introduced by background fluorescence originating from fluorophores outside the plane of interest and from autofluorescence of the specimen and optical components (including lens cements), both of which limit the contrast of specimen features with respect to the background.
Due to the background signal not associated with the specimen features, the signal-to-noise ratio actually decreases for very large pinhole sizes (or in the absence of a pinhole). In the theoretically ideal confocal arrangement, signal-to-background (S/B) ratio is greatest when the detector pinhole aperture has a diameter of zero. Because such an aperture would exclude signal as well as background, however, it has no practical application. In a useful microscope, the aperture size must be increased to increase signal-to-noise ratio. In general, an optimum aperture size exists that maximizes signal-to-noise ratio, while still maintaining adequate signal-to-background ratio for good image contrast.
Increasing incident laser power at the specimen is another mechanism that can potentially be utilized to increase signal level, and subsequently improve signal-to-noise ratio. In practice, however, any improvement through this strategy is limited by a phenomenon referred to as fluorophore saturation, in which fluorescence emission intensity reaches a maximum and does not increase with additional laser power input. This non-linear response results from utilizing laser illumination so intense that a significant fraction of the often-limited number of fluorophore molecules has been elevated to the excited state (depopulating the ground state). The effect is to lower the apparent fluorophore concentration, and the resulting unpredicted relationship between fluorophore concentration and emission intensity complicates the interpretation of data. The fluorescence signal can therefore be limited by bleaching or by saturation, with considerably different relative effects on signal-to-noise ratio, and with different limitations on the performance of various microscope configurations.
The signal intensity limitations due to bleaching or saturation are especially critical to fluorescence microscopy performed on biological materials, which is the most common application of confocal instruments. The phenomena responsible for the limited emission signal are related to excessive time and/or intensity of light exposure. With other contrast enhancing mechanisms utilizing reflected or transmitted light combined with staining or immuno-gold labeling, or methods exploiting phase contrast differences, similar limitations exist for laser intensity in that specimen damage is a possibility. However, bleaching is not a factor in non-fluorescence techniques, and there is no restriction on the acquisition of signal over a long period of time if heating or other effects of prolonged illumination do not damage the specimen.
Because microscope resolution is inseparable from contrast, and contrast is dependent upon signal-to-noise ratio, the threshold contrast required for visibility of specimen features is ultimately limited by the number of detected photons. With the limited number of photons typical of fluorescence microscopy, diffraction-limited resolution is never achieved in practical instrument operation, and it becomes essential that the number of photons is maximized by optimizing every element in the imaging sequence. With respect to the noise in the confocal imaging signal, shot noise, or photon noise, is the most important in that it poses the fundamental limit to the signal-to-noise ratio. The shot noise associated with intrinsic fluctuations in the arrival of photons from the signal is external to the detector itself and cannot be reduced. The contributions of fluctuations in the arrival of photons from the background (the background noise) can be reduced, and this is most commonly accomplished by limiting the background signal acceptance of the detector.
The intrinsic statistical variation in the detected photon signal is governed by a Poisson distribution function, which tends to a normal distribution when sufficiently large numbers of photons are involved. Such a distribution has the property that its mean value is equal to its variance. Since shot noise is equivalent to the square root of the variance, for a signal consisting of n photons, the signal-to-noise ratio is given by:
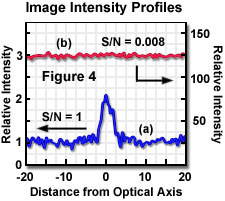
In an ideal microscope, only the optical shot noise limits the image quality. If no background signal is present, the signal-to-noise ratio is evaluated in a simple fashion, as illustrated by the equation above. In an actual microscope, the presence of background shot noise must also be considered and is added to the noise component in the relationship between signal and noise. If the ratio of signal to background is large, nearly all detected photons represent image information, and the signal-to-noise ratio approaches the value represented by the given equation. If the background contribution is large (small signal-to-background ratio), the desired signal may become lost in the high background shot noise, resulting in a signal-to-noise ratio approaching zero. The contrasting situations are illustrated in Figure 4, in which calculated image intensity profiles for a point source are presented for two different constant background signal levels. In Figure 4(a), the background intensity is equal to the intensity of the point source (above background) resulting in a signal-to-background ratio of 1. With a background level 125 times higher, as illustrated by the intensity profile of Figure 4(b), the resulting image would not allow discrimination of the point feature from the high background.
The optimum operation of the confocal microscope entails attempting to balance the conflicting requirements of utilizing an aperture in front of the detector, which is responsible for imparting the beneficial aspects of the confocal configuration, against the reduction in signal that the aperture also produces. With a circular (pinhole) aperture, increasing the diameter increases the total signal level, but decreases axial resolution, indicating that some compromise setting of aperture size is desirable. When fluorescence techniques are employed, the weak signal level is a distinct limitation to achieving optimum image quality. Although multiple-pass scanning and image averaging techniques can compensate for the low signal level, this defeats the advantage of fast-scan systems that might be applied to the study of dynamic processes in living organisms. An additional disadvantage of averaging techniques is that any noise produced by optical defects in the system, such as flare and scattering from optical components, is enhanced along with the signal, resulting in increased brightness without commensurate improvement in image quality.
The practical strategy for dealing with excessive background noise in the confocal fluorescence microscope configuration is to reduce the size of the detector aperture in order to exclude more of the background noise, thereby increasing both the signal-to-background and signal-to-noise ratios. As the aperture diameter is reduced, however, a point is reached at which the reduction of signal becomes more significant than the background reduction, and the signal-to-noise ratio decreases. It is obvious, therefore, that an aperture size can be found that maximizes signal-to-noise ratio, and that it can be determined on the basis of the relationship between signal and background. The aperture size that is determined to be optimal with regard to image quality will likely not correspond to maximum contrast or resolution, but does maximize specimen information in the image. The achievement of maximum useful signal, that which carries specimen information, is the basis for optimizing performance in fluorescence microscopy.
Laser illumination in the confocal microscope is focused into the specimen and distributed as the point spread function. Emitted fluorescence, after being collected and transferred to the image plane is again distributed as the point spread function of the optical system, having vertical and horizontal intensity profiles as illustrated in Figure 5. The widths of the point spread function intensity profiles are indicative of the microscope resolution. The longitudinal resolution is a function of the intensity distribution along the optical axis, while the point spread function at the focal point is the familiar Airy pattern, which determines lateral resolution. The first zero (minimum), occurring at a distance of 3.8 dimensionless units from the optical axis, corresponds to the Rayleigh criterion for lateral resolution. In order to achieve confocal operation, the emitted photons are spatially filtered by allowing detection of only those that pass through an aperture in front of the detector in the image plane. Maximum spatial filtering and background rejection occurs (theoretically) with an aperture radius (r) equal to zero. As r is increased to admit usable light levels, the confocal characteristics are reduced until, at large aperture radius, the microscope performs as a conventional wide field instrument.
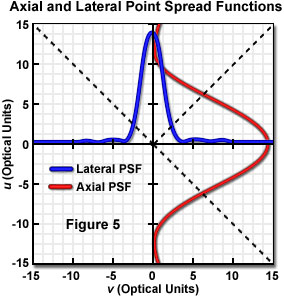
The intensity point spread function of an optical system takes on absolute dimensions that depend upon the imaging configuration, and that vary according to the magnification employed, the wavelength of the illumination, the numerical aperture of the optics, and the refractive index of the medium through which the light travels. It is customary for imaging properties of different microscopes and other optical systems to be represented utilizing dimensionless optical units that are independent of the optical system (for example, the distance of 3.8 units from the optical axis to the first minimum in the Airy pattern). These units are derived by normalizing the distances with the specific optical properties that are relevant in the lateral and longitudinal directions. Lateral distance values are normalized by the wavelength and numerical aperture, and similarly, longitudinal values are normalized by wavelength, numerical aperture, and refractive index of the specimen medium. For the purposes of evaluating imaging performance with respect to optical properties, it is useful to represent variables such as pinhole size in these dimensionless optical units, and an instrument-independent normalized pinhole radius can be defined in this manner.
Lateral and longitudinal distances (v and u, respectively) may be normalized to the width and axial dimension of the point spread function, by transformation to optical units employing the following equations:
in which r represents lateral distance from the optical axis, z is axial distance from the focal plane, NA is numerical aperture, n represents refractive index, and in each equation, k incorporates the wavelength (l) dependence as :
In order to evaluate the performance of the confocal instrument with varying detector pinhole size, a normalized pinhole radius v(d) can be derived from the previous equations as follows, for a pinhole of radius r(d):
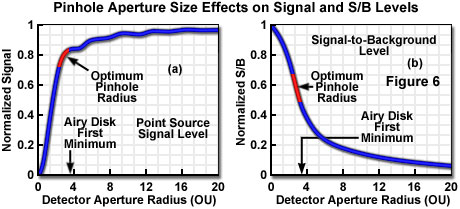
The fluorescence signal that can be collected from a point source in the focal plane when employing a detector aperture of radius v(d) can be calculated by considering the number of fluorophores in the point source, the absorption cross section, and the fluorescence quantum efficiency. The proportion of emitted photons reaching the image plane is distributed as the Airy pattern, which when integrated over the detector aperture radius and multiplied by the detection efficiency yields the actual collected signal. Figure 6(a) presents graphically a typical relationship between normalized collected signal from a theoretical point source and detector aperture radius, in optical units. With regard to signal lost by exclusion at the aperture, it is obvious that the small apertures required to produce the optimum confocal imaging performance would reject most of the emitted signal. Conversely, opening the aperture to admit a larger proportion of the emitted signal is only advantageous up to the point at which the contrast reduction from excess background becomes unacceptable. Several reported calculations place the range of apertures producing optimum signal-to-noise ratio at approximately 2 to 3 (indicated on the graph as a red portion of the curve, Figure 6(a)), depending upon the amount of background relative to signal. It is commonly considered desirable in many types of investigation to collect at least 50 percent of the total available fluorescence, and this is easily accomplished with apertures larger than approximately 2 optical units, while still retaining excellent image contrast.
Because of the combined requirements of achieving adequate signal level and sufficient background rejection to obtain optimum confocal performance it is necessary to evaluate both signal-to-noise and signal-to-background ratios. A number of different models for background (sometimes referred to as stray light) have been presented in the literature, and they differ in their applicability to different specimen types, instrument configurations, and whether reflected signal or fluorescence is detected for image formation. In some models, the background is assumed to have constant intensity over the entire detector plane, with the fraction passing through the pinhole being proportional to its area. Such models are found to be useful in describing confocal reflection configurations, for which significant background originates due to scattering within the microscope, and from reflections from optical elements within the light path.
Other models are considered to be more appropriate for fluorescence microscopy, and these differ in assumptions made about the extent of the spatial elements from which signal and background originate, which are in some cases quite arbitrary and variable. At least one model stresses the reduction of field size as a factor in reducing noise, and assumes a finite field size with infinite specimen thickness. In this case, if the background originates uniformly from a three-dimensional fluorescent specimen that is large compared to the point spread function, it may represent an appropriate model for fluorescence labeling with accompanying autofluorescence from background features. The details of computation of signal, background, signal-to-noise, and signal-to-background ratios appear in numerous literature presentations, and from these, certain generalizations are possible regarding optimization of factors such as pinhole size based on experimental and theoretical determinations of confocal imaging performance.
In a specimen having uniform distribution of fluorophores, because of the intensity distribution of the illuminating beam, the same fraction of excited fluorescence is collected from each focal plane in the conventional wide field microscope. As a consequence, the background signal increases linearly with specimen thickness. A crucial property of the confocal microscope, however, is that the detector aperture excludes the majority of light originating outside the focal plane, such that background signal level is nearly independent of specimen thickness if the thickness is large compared to the depth of field. When a uniform concentration of fluorophore is assumed, calculations of collected background signal for differing specimen thickness illustrate that circular detector pinhole radii greater or equal to the specimen thickness collect all of the specimen fluorescence, resulting in performance equivalent to the widefield microscope.
With smaller pinhole size, background is reduced from specimen planes farther than one-half the aperture radius from the focal plane, and as the pinhole radius is reduced below approximately one-fourth that of the specimen thickness, the background decreases linearly with aperture size. At aperture size less than approximately 4 optical units, beneficial confocal imaging properties are achieved with only about 1 percent of the background being admitted to the detector, at a moderate signal loss of perhaps 25 percent for specimen thickness as great as several hundred times the aperture size.
Taking into consideration the effect of specimen thickness and detector aperture size on background rejection allows calculation of the signal-to-background ratio for various values of each. When these calculations are conducted for varying specimen thickness with the ideal theoretical confocal configuration having a detector aperture of zero (maximizing signal-to-background ratio), the variation of signal-to-background has been shown to be essentially independent of specimen thickness for values greater than approximately 100 optical units. When signal-to-background is normalized to a value of one for a zero aperture radius, plotting is quantity as a function of aperture radius for thick samples results in a curve similar to that illustrated in Figure 6(b). The range of aperture sizes that maximize signal-to-noise ratio (as also illustrated in Figure 6(a)) is indicated by the red portion of the curve. Signal-to-background ratio is directly indicative of image contrast, and although maximum ratios cannot be achieved in practice since the aperture size must be increased to admit adequate signal, it is significant that reasonable contrast is obtainable at aperture sizes that produce optimum signal-to-noise ratio.
It should be noted that although experimental and theoretical evidence demonstrates that an optimum aperture size can be identified, which maximizes axial and lateral resolution in confocal microscopy, a number of factors contribute to the choice in compromised aperture size satisfying the imaging requirements in a particular situation. The optimum aperture size is commonly not the one that produces maximum resolution. Of greater significance in typical experiments is the number of information-carrying photons that can be discriminated from background signal and other noise sources within a practical time frame. The most important variables include the specimen characteristics (such as thickness), the signal level resulting from fluorescence emission or other image-forming signal, the noise level accompanying the signal, the time constraints on signal collection imposed by fluorophore bleaching or specimen changes, and the particular microscope configuration under consideration.
Contributing Authors
Kenneth R. Spring - Scientific Consultant, Lusby, Maryland, 20657.
Thomas J. Fellers and Michael W. Davidson - National High Magnetic Field Laboratory, 1800 East Paul Dirac Dr., The Florida State University, Tallahassee, Florida, 32310.